Matematica

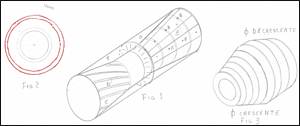Motore-generatore. Si tratta di un motore che nella parte rotorica avviene una combustione di Ossigeno e Idrogeno, derivata dall'elettrolisi dell'Acqua, l'espansione del gas combusto avviene tra gli incavi C dove il gas in espansione è trattenuto nei margini da determinate zone a tenuta.

Nella combustione il gas che si espande genera un momento torcente dovuto alla geometria quasi elicoidale.

Il generatore sarebbe una vera e propria pila Volta rotante B-A-E solidale con il rotore e dove B è ciò che emerge di un disco di Zinco, A è un disco di Rame, utili a produrre energia elettrica, E sarebbe un doppio condotto che funge da elettrodo di Nickel utile per lo svolgimento dell'elettrolisi, dove lo si trova ancorato ai dischi B, il tutto separato dai feltri imbevuti e rigenerati da Acido Carbonico per ottenere un pH adeguato, anche all’interno dell’Acqua per l’elettrolisi.

Sequenza di passaggi logici volti all’acquisizione della prova di aver
ottenuto la corrispondenza biunivoca tra direzioni e versi dimensionalmente formulati per gradienti secondo la relazione vigente tra Eulero verso Riemann, nonché Riemann verso Eulero.

In un libro ho letto di una questione relativa ad un quesito posto su come relazionarsi nei riguardi dei primi, intesi come parte della generalità dei numeri: la distribuzione dei numeri primi all’interno dei numeri naturali, segue una legge?

Ed, in caso affermativo, quale?

Ora, posto questo quesito, si dovrebbe dimostrare l’ipotesi di Riemann, cioè rivelare descrivendola, la distribuzione in un periodo precedente, ed in seguito postcedente.

Per porci nel caso più aderente ad una condizione prima, cioè riconducibile, e, accostabile ad un eventuale condizione riproducibile:

Il principale meccanismo di apprendimento di un computer si basa sul processo di memorizzazione delle informazioni.

Il tipo di codifica porta a stati del tipo tutto o niente, ma utilizzando una logica fuzzy si può memorizzare informazioni di tipo “sfumato” che consentono di gestire variabili soggette a incertezza e a conoscenza incompleta.

L'introduzione di algoritmi di tipo caotico consentono di rendere il sistema imprevedibile fornendo quella caratteristica tipicamente umana della contingenza e irripetibilità delle risposte. Le regole computazionali, con cui le connessioni tra i dati che costituiscono la memoria sono elaborati, potrebbero essere rafforzate o indebolite in modo da migliorare le prestazioni globali secondo criteri determinati dall'ambiente esterno.

È possibile utilizzare tecniche analoghe a quelle tipiche degli algoritmi genetici, in cui vi è una selezione naturale tra differenti procedure algoritmiche: l'algoritmo più efficace nasce per una specie di sopravvivenza del più adatto. In aggiunta vi possono essere elementi casuali incorporati nel modo in cui la macchina deve modificare le proprie prestazioni. In particolare è possibile utilizzare la variabile temporale per ottenere, tramite processi caotici, un effetto di pura casualità.

L'apprendimento può essere controllato da un esperto umano oppure basato su algoritmi di coerenza e non contraddizione. In particolare possono esistere due tipi di input: quello artificiale e quello naturale.